Rational Values
The Hurwitz zeta function occurs in a number of striking identities at rational values. In particular, values in terms of the Euler polynomials :
and
One also has
which holds for . Here, the and are defined by means of the Legendre chi function as
and
For integer values of ν, these may be expressed in terms of the Euler polynomials. These relations may be derived by employing the functional equation together with Hurwitz's formula, given above.
Read more about this topic: Hurwitz Zeta Function
Famous quotes containing the words rational and/or values:
“Plato—who may have understood better what forms the mind of man than do some of our contemporaries who want their children exposed only to “real” people and everyday events—knew what intellectual experience made for true humanity. He suggested that the future citizens of his ideal republic begin their literary education with the telling of myths, rather than with mere facts or so-called rational teachings.”
—Bruno Bettelheim (20th century)
“Our first line of defense in raising children with values is modeling good behavior ourselves. This is critical. How will our kids learn tolerance for others if our hearts are filled with hate? Learn compassion if we are indifferent? Perceive academics as important if soccer practice is a higher priority than homework?”
—Fred G. Gosman (20th century)

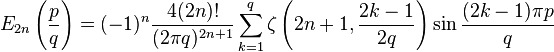
![\zeta\left(s,\frac{2p-1}{2q}\right) =
2(2q)^{s-1} \sum_{k=1}^q \left[
C_s\left(\frac{k}{q}\right) \cos \left(\frac{(2p-1)\pi k}{q}\right) +
S_s\left(\frac{k}{q}\right) \sin \left(\frac{(2p-1)\pi k}{q}\right)
\right]](http://upload.wikimedia.org/math/4/9/8/498855b49454d92f06ad65330d3b091c.png)