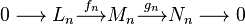Homological Algebra - Functoriality

Functoriality

A continuous map of topological spaces gives rise to a homomorphism between their nth homology groups for all n. This basic fact of algebraic topology finds a natural explanation through certain properties of chain complexes. Since it is very common to study several topological spaces simultaneously, in homological algebra one is led to simultaneous consideration of multiple chain complexes.

A morphism between two chain complexes, is a family of homomorphisms of abelian groups Fn:Cn → Dn that commute with the differentials, in the sense that Fn -1 • dnC = dnD • Fn for all n. A morphism of chain complexes induces a morphism of their homology groups, consisting of the homomorphisms Hn(F): Hn(C) → Hn(D) for all n. A morphism F is called a quasi-isomorphism if it induces an isomorphism on the nth homology for all n.

Many constructions of chain complexes arising in algebra and geometry, including singular homology, have the following functoriality property: if two objects X and Y are connected by a map f, then the associated chain complexes are connected by a morphism F = C(f) from to and moreover, the composition g • f of maps f: X → Y and g: Y → Z induces the morphism C(g • f) from to that coincides with the composition C(g) • C(f). It follows that the homology groups are functorial as well, so that morphisms between algebraic or topological objects give rise to compatible maps between their homology.

The following definition arises from a typical situation in algebra and topology. A triple consisting of three chain complexes and two morphisms between them, is called an exact triple, or a short exact sequence of complexes, and written as

0 \longrightarrow L_\bullet \stackrel{f}{\longrightarrow} M_\bullet \stackrel{g}{\longrightarrow} N_\bullet \longrightarrow 0,

if for any n, the sequence

0 \longrightarrow L_n \stackrel{f_n}{\longrightarrow} M_n \stackrel{g_n}{\longrightarrow} N_n \longrightarrow 0

is a short exact sequence of abelian groups. By definition, this means that fn is an injection, gn is a surjection, and Im fn = Ker gn. One of the most basic theorems of homological algebra, sometimes known as the zig-zag lemma, states that, in this case, there is a long exact sequence in homology

where the homology groups of L, M, and N cyclically follow each other, and δn are certain homomorphisms determined by f and g, called the connecting homomorphisms. Topological manifestations of this theorem include the Mayer–Vietoris sequence and the long exact sequence for relative homology.


Read more about this topic:  Homological Algebra