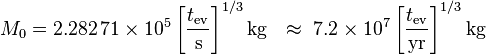Hawking Radiation - Black Hole Evaporation

Black Hole Evaporation

When particles escape, the black hole loses a small amount of its energy and therefore of its mass (mass and energy are related by Einstein's equation E = mc²).

The power emitted by a black hole in the form of Hawking radiation can easily be estimated for the simplest case of a nonrotating, non-charged Schwarzschild black hole of mass . Combining the formulas for the Schwarzschild radius of the black hole, the Stefan–Boltzmann law of black-body radiation, the above formula for the temperature of the radiation, and the formula for the surface area of a sphere (the black hole's event horizon), equation derivation:

Stefan–Boltzmann constant:

Schwarzschild radius:

Black hole surface gravity at the horizon:

Hawking radiation has a black-body (Planck) spectrum with a temperature T given by:

Hawking radiation temperature:

Schwarzschild sphere surface area of Schwarzschild radius :

Stefan–Boltzmann power law:

A black hole is a perfect black-body:

Stefan–Boltzmann–Schwarzschild–Hawking black hole radiation power law derivation:

Stefan–Boltzmann-Schwarzschild-Hawking power law:

Where is the energy outflow, is the reduced Planck constant, is the speed of light, and is the gravitational constant. It is worth mentioning that the above formula has not yet been derived in the framework of semiclassical gravity.

The power in the Hawking radiation from a solar mass black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'.

Under the assumption of an otherwise empty universe, so that no matter or cosmic microwave background radiation falls into the black hole, it is possible to calculate how long it would take for the black hole to dissipate:

Given that the power of the Hawking radiation is the rate of evaporation energy loss of the black hole:

Since the total energy E of the black hole is related to its mass M by Einstein's mass-energy formula:

We can then equate this to our above expression for the power:

This differential equation is separable, and we can write:

The black hole's mass is now a function M(t) of time t. Integrating over M from (the initial mass of the black hole) to zero (complete evaporation), and over t from zero to :

The evaporation time of a black hole is proportional to the cube of its mass:

The time that the black hole takes to dissipate is:

Where is the mass of the black hole.

The lower classical quantum limit for mass for this equation is equivalent to the Planck mass, .

Planck mass quantum black hole Hawking radiation evaporation time:

Where is the Planck time.

For a black hole of one solar mass ( = 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universe at 13.73 ± 0.12 x 109 years.

But for a black hole of 1011 kg, the evaporation time is 2.667 billion years. This is why some astronomers are searching for signs of exploding primordial black holes.

However, since the universe contains the cosmic microwave background radiation, in order for the black hole to dissipate, it must have a temperature greater than that of the present-day black-body radiation of the universe of 2.7 K = 2.3 × 10−4 eV. This implies that must be less than 0.8% of the mass of the Earth.

Cosmic microwave background radiation universe temperature:

Hawking total black hole mass:

Where, is the total Earth mass.

In common units,

So, for instance, a 1-second-lived black hole has a mass of 2.28 × 105 kg, equivalent to an energy of 2.05 × 1022 J that could be released by 5 × 106 megatons of TNT. The initial power is 6.84 × 1021 W.

Black hole evaporation has several significant consequences:

• Black hole evaporation produces a more consistent view of black hole thermodynamics, by showing how black holes interact thermally with the rest of the universe.
• Unlike most objects, a black hole's temperature increases as it radiates away mass. The rate of temperature increase is exponential, with the most likely endpoint being the dissolution of the black hole in a violent burst of gamma rays. A complete description of this dissolution requires a model of quantum gravity, however, as it occurs when the black hole approaches Planck mass and Planck radius.
• The simplest models of black hole evaporation lead to the black hole information paradox. The information content of a black hole appears to be lost when it dissipates, as under these models the Hawking radiation is random (it has no relation to the original information). A number of solutions to this problem have been proposed, including suggestions that Hawking radiation is perturbed to contain the missing information, that the Hawking evaporation leaves some form of remnant particle containing the missing information, and that information is allowed to be lost under these conditions.