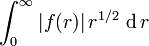Domain of Definition
The Hankel transform of a function f(r) is valid at every point at which f(r) is continuous provided that the function is defined in (0, ∞), is piecewise continuous and of bounded variation in every finite subinterval in (0, ∞), and the integral
is finite. However, like the Fourier Transform, the domain can be extended by a density argument to include some functions whose above integral is not finite, for example ; this extension will not be discussed in this article.
Read more about this topic: Hankel Transform
Famous quotes containing the words domain of, domain and/or definition:
“When it had long since outgrown his purely medical implications and become a world movement which penetrated into every field of science and every domain of the intellect: literature, the history of art, religion and prehistory; mythology, folklore, pedagogy, and what not.”
—Thomas Mann (1875–1955)
“When it had long since outgrown his purely medical implications and become a world movement which penetrated into every field of science and every domain of the intellect: literature, the history of art, religion and prehistory; mythology, folklore, pedagogy, and what not.”
—Thomas Mann (1875–1955)
“Although there is no universal agreement as to a definition of life, its biological manifestations are generally considered to be organization, metabolism, growth, irritability, adaptation, and reproduction.”
—The Columbia Encyclopedia, Fifth Edition, the first sentence of the article on “life” (based on wording in the First Edition, 1935)