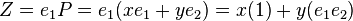Relationship With Other Formalisms
may be directly compared to vector algebra.
The even subalgebra of is isomorphic to the complex numbers, as may be seen by writing a vector P in terms of its components in an orthonormal basis and left multiplying by the basis vector e1, yielding
where we identify i ↦ e1e2 since
Similarly, the even subalgebra of with basis {1, e2e3, e3e1, e1e2} is isomorphic to the quaternions as may be seen by identifying i ↦ −e2e3, j ↦ −e3e1 and k ↦ −e1e2.
Every associative algebra has a matrix representation; the Pauli matrices are a representation of and the Dirac matrices are a representation of, showing the equivalence with matrix representations used by physicists.
Read more about this topic: Geometric Algebra
Famous quotes containing the words relationship with and/or relationship:
“Guilty, guilty, guilty is the chant divorced parents repeat in their heads. This constant reminder remains just below our consciousness. Nevertheless, its presence clouds our judgment, inhibits our actions, and interferes in our relationship with our children. Guilt is a major roadblock to building a new life for yourself and to being an effective parent.”
—Stephanie Marston (20th century)
“When a mother quarrels with a daughter, she has a double dose of unhappiness—hers from the conflict, and empathy with her daughter’s from the conflict with her. Throughout her life a mother retains this special need to maintain a good relationship with her daughter.”
—Terri Apter (20th century)