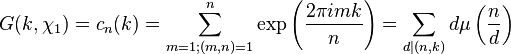Gaussian Period - Gauss Sums

As is discussed in more detail below, the Gaussian periods are closely related to another class of sums of roots of unity, now generally called Gauss sums (sometimes Gaussian sums). The quantity P − P* presented above is a quadratic Gauss sum mod p, the simplest non-trivial example of a Gauss sum. One observes that P − P* may also be written as

where here stands for the Legendre symbol (a/p), and the sum is taken over residue classes modulo p. More generally, given a Dirichlet character χ mod n, the Gauss sum mod n associated with χ is

For the special case of the principal Dirichlet character, the Gauss sum reduces to the Ramanujan sum:

$G(k,\chi_1) = c_n(k) = \sum_{m=1; (m,n)=1}^n \exp\left(\frac{2\pi imk}{n}\right) = \sum_{d|(n,k)} d\mu\left(\frac{n}{d}\right)$

where μ is the Möbius function.

The Gauss sums are ubiquitous in number theory; for example they occur significantly in the functional equations of L-functions. (Gauss sums are in a sense the finite field analogues of the gamma function.)

Read more about this topic: Gaussian Period

Famous quotes containing the word sums:

“At Timon’s villalet us pass a day,
Where all cry out,What sums are thrown away!’”
—Alexander Pope (1688–1744)