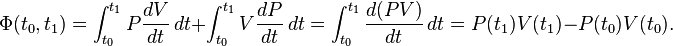Functions of State - Overview

Overview

A thermodynamic system is described by a number of thermodynamic parameters (e.g. temperature, volume, pressure) which are not necessarily independent. The number of parameters needed to describe the system is the dimension of the state space of the system . For example, a monatomic gas with a fixed number of particles is a simple case of a two-dimensional system . In this example, any system is uniquely specified by two parameters, such as pressure and volume, or perhaps pressure and temperature. These choices are equivalent. They are simply different coordinate systems in the two-dimensional thermodynamic state space. An analogous statement holds for higher dimensional spaces, as described by the state postulate.

When a system changes state continuously, it traces out a "path" in the state space. The path can be specified by noting the values of the state parameters as the system traces out the path, perhaps as a function of time, or some other external variable. For example, we might have the pressure and the volume as functions of time from time to . This will specify a path in our two dimensional state space example. We can now form all sorts of functions of time which we may integrate over the path. For example if we wish to calculate the work done by the system from time to time we calculate

It is clear that in order to calculate the work W in the above integral, we will have to know the functions and at each time, over the entire path. A state function is a function of the parameters of the system which only depends upon the parameters' values at the endpoints of the path. For example, suppose we wish to calculate the work plus the integral of over the path. We would have:

It can be seen that the integrand can be expressed as the exact differential of the function and that therefore, the integral can be expressed as the difference in the value of at the end points of the integration. The product is therefore a state function of the system.

By way of notation, we will specify the use of d to denote an exact differential. In other words, the integral of will be equal to . The symbol δ will be reserved for an inexact differential, which cannot be integrated without full knowledge of the path. For example will be used to denote an infinitesimal increment of work.

It is best to think of state functions as quantities or properties of a thermodynamic system, while non-state functions represent a process during which the state functions change. For example, the state function is proportional to the internal energy of an ideal gas, but the work is the amount of energy transferred as the system performs work. Internal energy is identifiable, it is a particular form of energy. Work is the amount of energy that has changed its form or location.