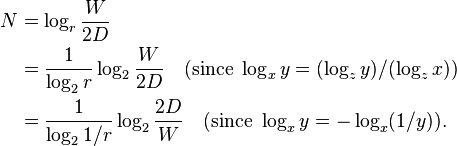Fitts's Law - Derivation

Derivation

Fitts's law can be derived from various models of motion. A very simple model, involving discrete, deterministic responses, is considered here. Although this model is overly simple, it provides some intuition for Fitts's law.

Assume that the user moves toward the target in a sequence of submovements. Each submovement requires a constant time t to execute, and moves a constant fraction 1-r of the remaining distance to the centre of the target, where 0 < r < 1. Thus, if the user is initially at a distance D from the target, the remaining distance after the first submovement is rD, and the remaining distance after the nth submovement is rnD. (In other words, the distance left to the target's centre is a function that decays exponentially over time.) Let N be the (possibly fractional) number of submovements required to fall within the target. Then,

Solving for N:

$\begin{align} N & = \log_r \frac{W}{2D} \\ & = \frac{1}{\log_2 r} \log_2 \frac{W}{2D}\quad(\text{since } \log_x y = (\log_z y)/(\log_z x)) \\ & = \frac{1}{\log_2 1/r} \log_2 \frac{2D}{W}\quad(\text{since } \log_x y = - \log_x(1/y)). \end{align}$

The time required for all submovements is:

$\begin{align} T = Nt & = \frac{t}{\log_2 1/r} \log_2 \frac{2D}{W} \\ & = \frac{t}{\log_2 1/r} + \frac{t}{\log_2 1/r} \log_2 \frac{D}{W}. \end{align}$

By defining appropriate constants a and b, this can be rewritten as

The above derivation is similar to one given in Card, Moran, and Newell (1983). For a critique of the deterministic iterative-corrections model, see Meyer et al. (1990).