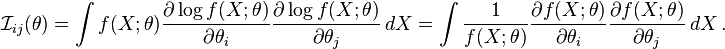Fisher Information - Distinction From The Hessian of The Entropy

Distinction From The Hessian of The Entropy

In certain cases, the Fisher Information matrix is the negative of the Hessian of the Shannon entropy. The cases where this explicitly holds is given below. A distribution's Shannon entropy

has as the negative of the entry of its Hessian:

$-\frac{\partial^2}{\partial\theta_i \partial\theta_j} \mathcal{H} = \int \left dX\,.$

In contrast, the entry of the Fisher information matrix is

$\mathcal{I}_{ij}(\theta) = \int f(X; \theta) \frac{\partial \log f(X; \theta)}{\partial\theta_i} \frac{\partial \log f(X; \theta)}{\partial\theta_j} \,dX = \int \frac{1}{f(X; \theta)} \frac{\partial f(X; \theta)}{\partial\theta_i} \frac{\partial f(X; \theta)}{\partial\theta_j} \,dX\,.$

The difference between the negative Hessian and the Fisher information is

$-\frac{\partial^2}{\partial\theta_i \, \partial\theta_j} \mathcal{H} - \mathcal{I}_{ij}(\theta) = \int \frac{\partial^2 f(X; \theta)}{\partial\theta_i \, \partial\theta_j} \left(1 + \log f(X; \theta) \right) dX\,.$

This extra term goes away if, instead, one considers the Hessian of the relative entropy instead of the Shannon entropy.

Read more about this topic: Fisher Information

Famous quotes containing the words distinction and/or entropy:

“But the iniquity of oblivion blindly scattereth her poppy, and deals with the memory of men without distinction to merit of perpetuity.”
—Thomas Browne (1605–1682)

“Just as the constant increase of entropy is the basic law of the universe, so it is the basic law of life to be ever more highly structured and to struggle against entropy.”
—Václav Havel (b. 1936)