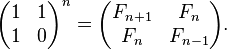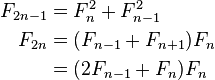Fibonacci Number - Matrix Form

Matrix Form

A 2-dimensional system of linear difference equations that describes the Fibonacci sequence is

\begin{align} {F_{k+2} \choose F_{k+1}} &= \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} {F_{k+1} \choose F_{k}} \\ \vec F_{k+1} &= A \vec F_{k} \end{align}

The eigenvalues of the matrix A are and, and the elements of the eigenvectors of A, and, are in the ratios and Using these facts, and the properties of eigenvalues, we can derive a direct formula for the nth element in the Fibonacci series as an analytic function of n:

The matrix has a determinant of −1, and thus it is a 2×2 unimodular matrix. This property can be understood in terms of the continued fraction representation for the golden ratio:

The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for, and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1.

The matrix representation gives the following closed expression for the Fibonacci numbers:

\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n = \begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{pmatrix}.

Taking the determinant of both sides of this equation yields Cassini's identity

Additionally, since for any square matrix A, the following identities can be derived:

\begin{align} {F_m}{F_n} + {F_{m-1}}{F_{n-1}} &= F_{m+n-1}\\ F_{n+1}F_{m} + F_n F_{m-1} &= F_{m+n} \end{align}

In particular, with ,

\begin{align} F_{2n-1} &= F_n^2 + F_{n-1}^2\\ F_{2n} &= (F_{n-1}+F_{n+1})F_n\\ &= (2F_{n-1}+F_n)F_n \end{align}

Read more about this topic:  Fibonacci Number

Famous quotes containing the words matrix and/or form:

    “As all historians know, the past is a great darkness, and filled with echoes. Voices may reach us from it; but what they say to us is imbued with the obscurity of the matrix out of which they come; and try as we may, we cannot always decipher them precisely in the clearer light of our day.”
    —Margaret Atwood (b. 1939)

    “Patience. A minor form of despair disguised as a virtue.”
    —Ambrose Bierce (1842–1914)