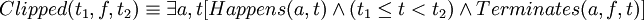Event Calculus - Domain-independent Axioms

Domain-independent Axioms

Like other languages for representing actions, the event calculus formalizes the correct evolution of the fluent via formulae telling the value of each fluent after an arbitrary action has been performed. The event calculus solves the frame problem in a way that is similar to the successor state axioms of the situation calculus: a fluent is true at time if and only if it has been made true in the past and has not been made false in the meantime.

HoldsAt(f,t) \leftarrow [Happens(a,t_1) \wedge Initiates(a,f,t_1) \wedge (t_1<t) \wedge \neg Clipped(t_1,f,t)]

This formula means that the fluent represented by the term is true at time if:

  1. an action has taken place: ;
  2. this took place in the past: ;
  3. this action has the fluent as an effect: ;
  4. the fluent has not been made false in the meantime:

A similar formula is used to formalize the opposite case in which a fluent is false at a given time. Other formulae are also needed for correctly formalizing fluents before they have been effects of an action. These formulae are similar to the above, but is replaced by .

The predicate, stating that a fluent has been made false during an interval, can be axiomatized, or simply taken as a shorthand, as follows:

Clipped(t_1,f,t_2) \equiv \exists a,t

Read more about this topic:  Event Calculus

Famous quotes containing the word axioms:

    “The axioms of physics translate the laws of ethics. Thus, “the whole is greater than its part;” “reaction is equal to action;” “the smallest weight may be made to lift the greatest, the difference of weight being compensated by time;” and many the like propositions, which have an ethical as well as physical sense. These propositions have a much more extensive and universal sense when applied to human life, than when confined to technical use.”
    —Ralph Waldo Emerson (1803–1882)