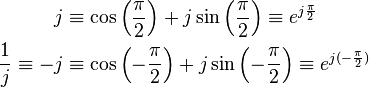Electrical Impedance - Device Examples

Device Examples

The impedance of an ideal resistor is purely real and is referred to as a resistive impedance:

In this case, the voltage and current waveforms are proportional and in phase.

Ideal inductors and capacitors have a purely imaginary reactive impedance:

the impedance of inductors increases as frequency increases;

the impedance of capacitors decreases as frequency increases;

In both cases, for an applied sinusoidal voltage, the resulting current is also sinusoidal, but in quadrature, 90 degrees out of phase with the voltage. However, the phases have opposite signs: in an inductor, the current is lagging; in a capacitor the current is leading.

Note the following identities for the imaginary unit and its reciprocal:

\begin{align} j &\equiv \cos{\left( \frac{\pi}{2}\right)} + j\sin{\left( \frac{\pi}{2}\right)} \equiv e^{j \frac{\pi}{2}} \\ \frac{1}{j} \equiv -j &\equiv \cos{\left(-\frac{\pi}{2}\right)} + j\sin{\left(-\frac{\pi}{2}\right)} \equiv e^{j(-\frac{\pi}{2})} \end{align}

Thus the inductor and capacitor impedance equations can be rewritten in polar form:

\begin{align} Z_L &= \omega Le^{j\frac{\pi}{2}} \\ Z_C &= \frac{1}{\omega C}e^{j\left(-\frac{\pi}{2}\right)} \end{align}

The magnitude gives the change in voltage amplitude for a given current amplitude through the impedance, while the exponential factors give the phase relationship.

Read more about this topic:  Electrical Impedance

Famous quotes containing the words device and/or examples:

    “One good reason for the popularity of “reductionism” among the philosophical outposts of the Western Establishment is that it can be, and is, used as a device for trying to take the wind, so to speak, out of the sails of Marxism.... In essence reductionism is a kind of anti-Marxist caricature of Marxist determinism. It is what anti-Marxists pretend that Marxist determinism is.”
    —Claud Cockburn (1904–1981)

    “Histories are more full of examples of the fidelity of dogs than of friends.”
    —Alexander Pope (1688–1744)