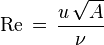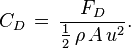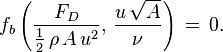Drag Equation

The drag equation may be derived to within a multiplicative constant by the method of dimensional analysis. If a moving fluid meets an object, it exerts a force on the object, according to a complicated (and not completely understood) law. Suppose that the variables involved – under some conditions – are the:

  • speed u,
  • fluid density ρ,
  • viscosity ν of the fluid,
  • size of the body, expressed in terms of its frontal area A, and
  • drag force FD.

Using the algorithm of the Buckingham π theorem, these five variables can be reduced to two dimensionless parameters:

  • drag coefficient CD and
  • Reynolds number Re.

Alternatively, the dimensionless parameters via direct manipulation of the underlying differential equations.

That this is so becomes apparent when the drag force FD is expressed as part of a function of the other variables in the problem:

f_a(F_D,\, u,\, A,\, \rho,\, \nu)\, =\, 0. \,

This rather odd form of expression is used because it does not assume a one-to-one relationship. Here, fa is some (as-yet-unknown) function that takes five arguments. Now the right-hand side is zero in any system of units; so it should be possible to express the relationship described by fa in terms of only dimensionless groups.

There are many ways of combining the five arguments of fa to form dimensionless groups, but the Buckingham π theorem states that there will be two such groups. The most appropriate are the Reynolds number, given by

\mathrm{Re}\, =\, \frac{u\,\sqrt{A}}{\nu}

and the drag coefficient, given by

C_D\, =\, \frac{F_D}{\frac12\, \rho\, A\, u^2}.

Thus the function of five variables may be replaced by another function of only two variables:

f_b\left( \frac{F_D}{\frac12\, \rho\, A\, u^2},\, \frac{u\, \sqrt{A}}{\nu} \right)\, =\, 0.

where fb is some function of two arguments. The original law is then reduced to a law involving only these two numbers.

Because the only unknown in the above equation is the drag force FD, it is possible to express it as

\frac{F_D}{\frac12\, \rho\, A\, u^2}\, =\, f_c\left( \frac{u\, \sqrt{A}}{\nu} \right)

or

F_D\, =\, \tfrac12\, \rho\, A\, u^2\, f_c(R_e), \, and with

Thus the force is simply ½ ρ A u2 times some (as-yet-unknown) function fc of the Reynolds number Re – a considerably simpler system than the original five-argument function given above.

Dimensional analysis thus makes a very complex problem (trying to determine the behavior of a function of five variables) a much simpler one: the determination of the drag as a function of only one variable, the Reynolds number.

The analysis also gives other information for free, so to speak. The analysis shows that, other things being equal, the drag force will be proportional to the density of the fluid. This kind of information often proves to be extremely valuable, especially in the early stages of a research project.

To empirically determine the Reynolds number dependence, instead of experimenting on huge bodies with fast-flowing fluids (such as real-size airplanes in wind-tunnels), one may just as well experiment on small models with more viscous and higher velocity fluids, because these two systems are similar.

Famous quotes containing the words drag and/or equation:

    “I know those little phrases that seem so innocuous and, once you let them in, pollute the whole of speech. Nothing is more real than nothing. They rise up out of the pit and know no rest until they drag you down into its dark.”
    —Samuel Beckett (1906–1989)

    “A nation fights well in proportion to the amount of men and materials it has. And the other equation is that the individual soldier in that army is a more effective soldier the poorer his standard of living has been in the past.”
    —Norman Mailer (b. 1923)