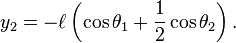Double Pendulum - Analysis

Analysis

Several variants of the double pendulum may be considered; the two limbs may be of equal or unequal lengths and masses, they may be simple pendulums or compound pendulums (also called complex pendulums) and the motion may be in three dimensions or restricted to the vertical plane. In the following analysis, the limbs are taken to be identical compound pendulums of length and mass, and the motion is restricted to two dimensions.

In a compound pendulum, the mass is distributed along its length. If the mass is evenly distributed, then the center of mass of each limb is at its midpoint, and the limb has a moment of inertia of about that point.

It is convenient to use the angles between each limb and the vertical as the generalized coordinates defining the configuration of the system. These angles are denoted θ1 and θ2. The position of the center of mass of each rod may be written in terms of these two coordinates. If the origin of the Cartesian coordinate system is taken to be at the point of suspension of the first pendulum, then the center of mass of this pendulum is at:

x_1 = \frac{\ell}{2} \sin \theta_1,
y_1 = -\frac{\ell}{2} \cos \theta_1

and the center of mass of the second pendulum is at

x_2 = \ell \left ( \sin \theta_1 + \frac{1}{2} \sin \theta_2 \right ),
y_2 = -\ell \left ( \cos \theta_1 + \frac{1}{2} \cos \theta_2 \right ).

This is enough information to write out the Lagrangian.

Read more about this topic:  Double Pendulum

Famous quotes containing the word analysis:

    “Ask anyone committed to Marxist analysis how many angels on the head of a pin, and you will be asked in return to never mind the angels, tell me who controls the production of pins.”
    —Joan Didion (b. 1934)

    “Whatever else American thinkers do, they psychologize, often brilliantly. The trouble is that psychology only takes us so far. The new interest in families has its merits, but it will have done us all a disservice if it turns us away from public issues to private matters. A vision of things that has no room for the inner life is bankrupt, but a psychology without social analysis or politics is both powerless and very lonely.”
    —Joseph Featherstone (20th century)