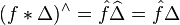Dirac Delta Function - Dirac Comb

Dirac Comb

A so-called uniform "pulse train" of Dirac delta measures, which is known as a Dirac comb, or as the Shah distribution, creates a sampling function, often used in digital signal processing (DSP) and discrete time signal analysis. The Dirac comb is given as the infinite sum, whose limit is understood in the distribution sense,

which is a sequence of point masses at each of the integers.

Up to an overall normalizing constant, the Dirac comb is equal to its own Fourier transform. This is significant because if ƒ is any Schwartz function, then the periodization of ƒ is given by the convolution

In particular,

(f*\Delta)^\wedge = \hat{f}\widehat{\Delta} = \hat{f} \Delta

is precisely the Poisson summation formula.

Read more about this topic:  Dirac Delta Function

Famous quotes containing the word comb:

    “And still we wear our uniforms, follow
    The cracked cry of the bugles, comb and brush
    Our pride and prejudice, doctor the sallow
    Initial ardor, wish to keep it fresh.
    Still we applaud the President’s voice and face.”
    —Gwendolyn Brooks (b. 1917)