Del in Cylindrical and Spherical Coordinates - Note

Note

  • This page uses standard physics notation. For spherical coordinates, is the angle between the z axis and the radius vector connecting the origin to the point in question. is the angle between the projection of the radius vector onto the x-y plane and the x axis. Some sources reverse the definitions of and, so the meaning should be inferred from the context.
  • The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) owing to its domain and image. The classical arctan(y/x) has an image of (-π/2, +π/2), whereas atan2(y, x) is defined to have an image of (-π, π]. (The expressions for the Del in spherical coordinates may need to be corrected)
Table with the del operator in cylindrical, spherical and parabolic cylindrical coordinates
Operation Cartesian coordinates (x,y,z) Cylindrical coordinates (ρ,φ,z) Spherical coordinates (r,θ,φ) Parabolic cylindrical coordinates (σ,τ,z)
Definition
of
coordinates		 \begin{matrix} \rho & = & \sqrt{x^2+y^2} \\ \phi & = & \arctan(y/x) \\ z & = & z \end{matrix} \begin{matrix} x & = & \rho\cos\phi \\ y & = & \rho\sin\phi \\ z & = & z \end{matrix} \begin{matrix} x & = & r\sin\theta\cos\phi \\ y & = & r\sin\theta\sin\phi \\ z & = & r\cos\theta \end{matrix} \begin{matrix} x & = & \sigma \tau\\ y & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}
\begin{matrix} r & = & \sqrt{x^2+y^2+z^2} \\ \theta & = & \arccos(z/r)\\ \phi & = & \arctan(y/x) \\ \end{matrix} \begin{matrix} r & = & \sqrt{\rho^2 + z^2} \\ \theta & = & \arctan{(\rho/z)}\\ \phi & = & \phi \end{matrix} \begin{matrix} \rho & = & r\sin(\theta) \\ \phi & = & \phi\\ z & = & r\cos(\theta) \end{matrix} \begin{matrix} \rho\cos\phi & = & \sigma \tau\\ \rho\sin\phi & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}
Definition
of
unit
vectors		 \begin{matrix} \boldsymbol{\hat \rho} & = & \frac{x}{\sqrt{x^2+y^2}}\mathbf{\hat x}+\frac{y}{\sqrt{x^2+y^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\phi} & = & -\frac{y}{\sqrt{x^2+y^2}}\mathbf{\hat x}+\frac{x}{\sqrt{x^2+y^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix} \begin{matrix} \mathbf{\hat x} & = & \cos\phi\boldsymbol{\hat \rho}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\phi\boldsymbol{\hat \rho}+\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix} \begin{matrix} \mathbf{\hat x} & = & \sin\theta\cos\phi\boldsymbol{\hat r}+\cos\theta\cos\phi\boldsymbol{\hat\theta}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\theta\sin\phi\boldsymbol{\hat r}+\cos\theta\sin\phi\boldsymbol{\hat\theta}+\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta \boldsymbol{\hat r}-\sin\theta \boldsymbol{\hat\theta} \\ \end{matrix} \begin{matrix} \boldsymbol{\hat \sigma} & = & \frac{\tau}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat x}-\frac{\sigma}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\tau} & = & \frac{\sigma}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat x}+\frac{\tau}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}
\begin{matrix} \mathbf{\hat r} &=& \frac{ x }{\sqrt{x^2+y^2+z^2}}\mathbf{\hat x}\!+\!\frac{ y }{\sqrt{x^2+y^2+z^2}}\mathbf{\hat y}\!+\!\frac{z}{\sqrt{x^2+y^2+z^2}}\mathbf{\hat z}\\ \boldsymbol{\hat\theta} &=& \frac{ xz }{\sqrt{x^2+y^2+z^2}\sqrt{x^2+y^2}}\mathbf{\hat x}\!+\!\frac{ yz }{\sqrt{x^2+y^2+z^2}\sqrt{x^2+y^2}}\mathbf{\hat y}\!-\!\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+z^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} &=& -\frac{y}{\sqrt{x^2+y^2}}\mathbf{\hat x}+\frac{x}{\sqrt{x^2+y^2}}\mathbf{\hat y} \end{matrix} \begin{matrix} \mathbf{\hat r} & = & \frac{\rho}{\sqrt{\rho^2 +z^2}}\boldsymbol{\hat \rho}+\frac{ z}{\sqrt{\rho^2 +z^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\theta} & = & \frac{z }{\sqrt{\rho^2 +z^2}}\boldsymbol{\hat \rho}-\frac{\rho}{\sqrt{\rho^2 +z^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \end{matrix} \begin{matrix} \boldsymbol{\hat \rho} & = & \sin\theta\mathbf{\hat r}+\cos\theta\boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta\mathbf{\hat r}-\sin\theta\boldsymbol{\hat\theta} \\ \end{matrix} \begin{matrix} \end{matrix}
A vector field
Gradient {\partial f \over \partial x}\mathbf{\hat x} + {\partial f \over \partial y}\mathbf{\hat y} + {\partial f \over \partial z}\mathbf{\hat z} {\partial f \over \partial \rho}\boldsymbol{\hat \rho} + {1 \over \rho}{\partial f \over \partial \phi}\boldsymbol{\hat \phi} + {\partial f \over \partial z}\boldsymbol{\hat z} {\partial f \over \partial r}\boldsymbol{\hat r} + {1 \over r}{\partial f \over \partial \theta}\boldsymbol{\hat \theta} + {1 \over r\sin\theta}{\partial f \over \partial \phi}\boldsymbol{\hat \phi}
Divergence {1 \over \rho}{\partial \left( \rho A_\rho \right) \over \partial \rho} + {1 \over \rho}{\partial A_\phi \over \partial \phi} + {\partial A_z \over \partial z} {1 \over r^2}{\partial \left( r^2 A_r \right) \over \partial r} + {1 \over r\sin\theta}{\partial \over \partial \theta} \left( A_\theta\sin\theta \right) + {1 \over r\sin\theta}{\partial A_\phi \over \partial \phi}
Curl \begin{matrix} \displaystyle\left({\partial A_z \over \partial y} - {\partial A_y \over \partial z}\right) \mathbf{\hat x} & + \\ \displaystyle\left({\partial A_x \over \partial z} - {\partial A_z \over \partial x}\right) \mathbf{\hat y} & + \\ \displaystyle\left({\partial A_y \over \partial x} - {\partial A_x \over \partial y}\right) \mathbf{\hat z} & \ \end{matrix} \begin{matrix} \displaystyle\left({1 \over \rho}{\partial A_z \over \partial \phi} - {\partial A_\phi \over \partial z}\right) \boldsymbol{\hat \rho} & + \\ \displaystyle\left({\partial A_\rho \over \partial z} - {\partial A_z \over \partial \rho}\right) \boldsymbol{\hat \phi} & + \\ \displaystyle{1 \over \rho}\left({\partial \left( \rho A_\phi \right) \over \partial \rho} - {\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat z} & \ \end{matrix} \begin{matrix} \displaystyle{1 \over r\sin\theta}\left({\partial \over \partial \theta} \left( A_\phi\sin\theta \right) - {\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat r} & + \\ \displaystyle{1 \over r}\left({1 \over \sin\theta}{\partial A_r \over \partial \phi} - {\partial \over \partial r} \left( r A_\phi \right) \right) \boldsymbol{\hat \theta} & + \\ \displaystyle{1 \over r}\left({\partial \over \partial r} \left( r A_\theta \right) - {\partial A_r \over \partial \theta}\right) \boldsymbol{\hat \phi} & \ \end{matrix} \begin{matrix} \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}{\partial A_z \over \partial \tau} - {\partial A_\tau \over \partial z}\right) \boldsymbol{\hat \sigma} & - \\ \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}{\partial A_z \over \partial \sigma}- {\partial A_\sigma \over \partial z}\right) \boldsymbol{\hat \tau} & + \\ \displaystyle\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}\left({\partial \left( \sqrt{\sigma^{2} + \tau^{2}} A_\sigma \right) \over \partial \tau} - {\partial \left( \sqrt{\sigma^{2} + \tau^{2}} A_\tau \right) \over \partial \sigma}\right) \boldsymbol{\hat z} & \ \end{matrix}
Laplace operator {1 \over \rho}{\partial \over \partial \rho}\left(\rho {\partial f \over \partial \rho}\right) + {1 \over \rho^2}{\partial^2 f \over \partial \phi^2} + {\partial^2 f \over \partial z^2} {1 \over r^2}{\partial \over \partial r}\!\left(r^2 {\partial f \over \partial r}\right) \!+\!{1 \over r^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta {\partial f \over \partial \theta}\right) \!+\!{1 \over r^2\!\sin^2\theta}{\partial^2 f \over \partial \phi^2} \frac{1}{\sigma^{2} + \tau^{2}} \left( \frac{\partial^{2} f}{\partial \sigma^{2}} + \frac{\partial^{2} f}{\partial \tau^{2}} \right) + \frac{\partial^{2} f}{\partial z^{2}}
Vector Laplacian \begin{matrix} \displaystyle\left(\Delta A_\rho - {A_\rho \over \rho^2} - {2 \over \rho^2}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat \rho} & + \\ \displaystyle\left(\Delta A_\phi - {A_\phi \over \rho^2} + {2 \over \rho^2}{\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat\phi} & + \\ \displaystyle\left(\Delta A_z \right) \boldsymbol{\hat z} & \ \end{matrix} \begin{matrix} \left(\Delta A_r - {2 A_r \over r^2} - {2 \over r^2\sin\theta}{\partial \left(A_\theta \sin\theta\right) \over \partial\theta} - {2 \over r^2\sin\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat r} & + \\ \left(\Delta A_\theta - {A_\theta \over r^2\sin^2\theta} + {2 \over r^2}{\partial A_r \over \partial \theta} - {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat\theta} & + \\ \left(\Delta A_\phi - {A_\phi \over r^2\sin^2\theta} + {2 \over r^2\sin\theta}{\partial A_r \over \partial \phi} + {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat\phi} & \end{matrix}
Material derivative


\begin{matrix} \displaystyle\left(A_x \frac{\partial B_x}{\partial x}+A_y \frac{\partial B_x}{\partial y} + A_z \frac{\partial B_x}{\partial z}\right)\boldsymbol{\hat{x}} & + \\ \displaystyle\left(A_x \frac{\partial B_y}{\partial x}+A_y \frac{\partial B_y}{\partial y} + A_z \frac{\partial B_y}{\partial z}\right)\boldsymbol{\hat{y}} & + \\ \displaystyle\left(A_x \frac{\partial B_z}{\partial x}+A_y \frac{\partial B_z}{\partial y} + A_z \frac{\partial B_z}{\partial z}\right)\boldsymbol{\hat{z}} \end{matrix}


\begin{matrix} \left(A_\rho \frac{\partial B_\rho}{\partial \rho}+\frac{A_\phi}{\rho}\frac{\partial B_\rho}{\partial \phi}+A_z\frac{\partial B_\rho}{\partial z}-\frac{A_\phi B_\phi}{\rho}\right) \boldsymbol{\hat\rho} \!+\!\\ \left(A_\rho \frac{\partial B_\phi}{\partial \rho}+\frac{A_\phi}{\rho}\frac{\partial B_\phi}{\partial \phi}+A_z\frac{\partial B_\phi}{\partial z}+\frac{A_\phi B_\rho}{\rho}\right) \boldsymbol{\hat\phi}\!+\!\\ \left(A_\rho \frac{\partial B_z }{\partial \rho}+\frac{A_\phi}{\rho}\frac{\partial B_z }{\partial \phi}+A_z\frac{\partial B_z }{\partial z} \right) \boldsymbol{\hat z} \end{matrix}


\begin{matrix} \left(A_r \frac{\partial B_r}{\partial r}\!+\!\frac{A_\theta}{r}\frac{\partial B_r}{\partial \theta}\!+\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_r}{\partial \phi}\!-\!\frac{A_\theta B_\theta\!+\!A_\phi B_\phi}{r}\right) \boldsymbol{\hat r} \!+\!\\ \left(A_r \frac{\partial B_\theta}{\partial r}\!+\!\frac{A_\theta}{r}\frac{\partial B_\theta}{\partial \theta}\!+\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_\theta}{\partial \phi}\!+\!\frac{A_\theta B_r}{r}-\frac{A_\phi B_\phi\cot(\theta)}{r}\right) \boldsymbol{\hat\theta} \!+\!\\ \left(A_r \frac{\partial B_\phi}{\partial r}\!+\!\frac{A_\theta}{r}\frac{\partial B_\phi}{\partial \theta}\!+\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_\phi}{\partial \phi}\!+\!\frac{A_\phi B_r}{r}\!+\!\frac{A_\phi B_\theta \cot(\theta)}{r}\right)\boldsymbol{\hat\phi} \end{matrix}
Differential displacement
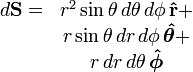Differential normal area \begin{matrix}d\mathbf{S} = &dy\,dz\,\mathbf{\hat x} + \\ &dx\,dz\,\mathbf{\hat y} + \\ &dx\,dy\,\mathbf{\hat z}\end{matrix} \begin{matrix} d\mathbf{S} = & \rho\, d\phi\, dz\,\boldsymbol{\hat \rho} + \\ & d\rho \,dz\,\boldsymbol{\hat \phi} + \\ & \rho \,d\rho d\phi \,\mathbf{\hat z} \end{matrix} \begin{matrix} d\mathbf{S} = & r^2 \sin\theta \,d\theta \,d\phi \,\mathbf{\hat r} + \\ & r\sin\theta \,dr\,d\phi \,\boldsymbol{\hat \theta} + \\ & r\,dr\,d\theta\,\boldsymbol{\hat \phi} \end{matrix} \begin{matrix} d\mathbf{S} = & \sqrt{\sigma^{2} + \tau^{2}}, d\tau\, dz\,\boldsymbol{\hat \sigma} + \\ & \sqrt{\sigma^{2} + \tau^{2}} d\sigma\,dz\,\boldsymbol{\hat \tau} + \\ & \sigma^{2} + \tau^{2} d\sigma, d\tau \,\mathbf{\hat z} \end{matrix}
Differential volume
Non-trivial calculation rules:
  1. (Laplacian)
  2. \operatorname{curl\ curl\ } \mathbf{A} = \nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A} (using Lagrange's formula for the cross product)

Read more about this topic:  Del In Cylindrical And Spherical Coordinates

Famous quotes containing the word note:

    “In our Mechanics’ Fair, there must be not only bridges, ploughs, carpenter’s planes, and baking troughs, but also some few finer instruments,—rain-gauges, thermometers, and telescopes; and in society, besides farmers, sailors, and weavers, there must be a few persons of purer fire kept specially as gauges and meters of character; persons of a fine, detecting instinct, who note the smallest accumulations of wit and feeling in the bystander.”
    —Ralph Waldo Emerson (1803–1882)

    “In it he proves that all things are true and states how the truths of all contradictions may be reconciled physically, such as for example that white is black and black is white; that one can be and not be at the same time; that there can be hills without valleys; that nothingness is something and that everything, which is, is not. But take note that he proves all these unheard-of paradoxes without any fallacious or sophistical reasoning.”
    —Savinien Cyrano De Bergerac (1619–1655)

    “Poor old Jonathan Bing
    Went home and addressed a short note to the King:
    If you please will excuse me
    I won’t come to tea;
    For home’s the best place for
    All people like me!”
    —Beatrice Curtis Brown (1901–1974)