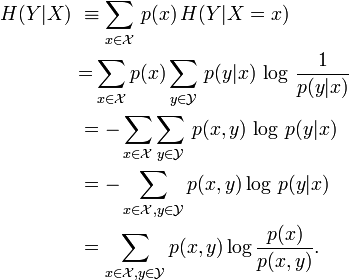Conditional Entropy - Definition

Definition

If is the entropy of the variable conditioned on the variable taking a certain value, then is the result of averaging over all possible values that may take.

Given discrete random variable with support and with support, the conditional entropy of given is defined as:

\begin{align} H(Y|X)\ &\equiv \sum_{x\in\mathcal X}\,p(x)\,H(Y|X=x)\\ &{=}\sum_{x\in\mathcal X}p(x)\sum_{y\in\mathcal Y}\,p(y|x)\,\log\, \frac{1}{p(y|x)}\\ &=-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}\,p(x,y)\,\log\,p(y|x)\\ &=-\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log\,p(y|x)\\ &=\sum_{x\in\mathcal X, y\in\mathcal Y}p(x,y)\log \frac {p(x)} {p(x,y)}. \\ \end{align}


Note: The supports of X and Y can be replaced by their domains if it is understood that should be treated as being equal to zero.

if and only if the value of is completely determined by the value of . Conversely, if and only if and are independent random variables.

Read more about this topic:  Conditional Entropy

Famous quotes containing the word definition:

    “Scientific method is the way to truth, but it affords, even in
    principle, no unique definition of truth. Any so-called pragmatic
    definition of truth is doomed to failure equally.”
    —Willard Van Orman Quine (b. 1908)

    “No man, not even a doctor, ever gives any other definition of what a nurse should be than this—”devoted and obedient.” This definition would do just as well for a porter. It might even do for a horse. It would not do for a policeman.”
    —Florence Nightingale (1820–1910)

    “The man who knows governments most completely is he who troubles himself least about a definition which shall give their essence. Enjoying an intimate acquaintance with all their particularities in turn, he would naturally regard an abstract conception in which these were unified as a thing more misleading than enlightening.”
    —William James (1842–1910)