Example
The classical differentiation operator
defined on the set D(T) of all continuously differentiable functions f on the closed interval is an unbounded operator H → H where H=L2 is the Hilbert space of all square integrable functions on (more exactly, equivalence classes; the functions must be measurable, either real-valued or complex-valued). The definition of T is correct, since a continuous (the more so, continuously differentiable) function cannot vanish almost everywhere, unless it vanishes everywhere.
This is a linear operator, since a linear combination af+bg of two continuously differentiable functions f, g is also continuously differentiable, and
The operator is not bounded. For example, the functions fn defined on by satisfy but
The operator is densely defined, and not closed.
The same operator can be treated as an operator B → B for many Banach spaces B and is still not bounded. However, it is bounded as an operator B1 → B2 for some pairs of Banach spaces B1, B2, and also as operator B → B for some topological vector spaces B. As an example consider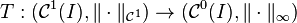 
, for some open interval and the norm being .
Read more about this topic: Closed Operator
Famous quotes containing the word example:
“Our intellect is not the most subtle, the most powerful, the most appropriate, instrument for revealing the truth. It is life that, little by little, example by example, permits us to see that what is most important to our heart, or to our mind, is learned not by reasoning but through other agencies. Then it is that the intellect, observing their superiority, abdicates its control to them upon reasoned grounds and agrees to become their collaborator and lackey.”
—Marcel Proust (1871–1922)