Classical Test Theory - Evaluating Tests and Scores: Reliability

Evaluating Tests and Scores: Reliability

Reliability cannot be estimated directly since that would require one to know the true scores, which according to classical test theory is impossible. However, estimates of reliability can be obtained by various means. One way of estimating reliability is by constructing a so-called parallel test. The fundamental property of a parallel test is that it yields the same true score and the same observed score variance as the original test for every individual. If we have parallel tests x and x', then this means that

and

Under these assumptions, it follows that the correlation between parallel test scores is equal to reliability (see Lord & Novick, 1968, Ch. 2, for a proof).

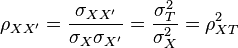
{\rho}_{XX'}= \frac{{\sigma}_{XX'}}{{\sigma}_X{\sigma}_{X'}}= \frac{ {\sigma}_T^2 }{ {\sigma}_X^2 }= {\rho}_{XT}^2

Using parallel tests to estimate reliability is cumbersome because parallel tests are very hard to come by. In practice the method is rarely used. Instead, researchers use a measure of internal consistency known as Cronbach's . Consider a test consisting of items, . The total test score is defined as the sum of the individual item scores, so that for individual

Then Cronbach's alpha equals

Cronbach's can be shown to provide a lower bound for reliability under rather mild assumptions. Thus, the reliability of test scores in a population is always higher than the value of Cronbach's in that population. Thus, this method is empirically feasible and, as a result, it is very popular among researchers. Calculation of Cronbach's is included in many standard statistical packages such as SPSS and SAS.

As has been noted above, the entire exercise of classical test theory is done to arrive at a suitable definition of reliability. Reliability is supposed to say something about the general quality of the test scores in question. The general idea is that, the higher reliability is, the better. Classical test theory does not say how high reliability is supposed to be. Too high a value for, say over .9, indicates redundancy of items. Around .8 is recommended for personality research, while .9+ is desirable for individual high-stakes testing. These 'criteria' are not based on formal arguments, but rather are the result of convention and professional practice. The extent to which they can be mapped to formal principles of statistical inference is unclear.

Read more about this topic:  Classical Test Theory

Famous quotes containing the words evaluating and/or tests:

    “Evaluation is creation: hear it, you creators! Evaluating is itself the most valuable treasure of all that we value. It is only through evaluation that value exists: and without evaluation the nut of existence would be hollow. Hear it, you creators!”
    —Friedrich Nietzsche (1844–1900)

    “Letters have to pass two tests before they can be classed as good: they must express the personality both of the writer and of the recipient.”
    —E.M. (Edward Morgan)