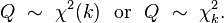Chi-squared Distribution - Definition

Definition

If Z1, ..., Zk are independent, standard normal random variables, then the sum of their squares,

Q\ = \sum_{i=1}^k Z_i^2,

is distributed according to the chi-squared distribution with k degrees of freedom. This is usually denoted as

Q\ \sim\ \chi^2(k)\ \ \text{or}\ \ Q\ \sim\ \chi^2_k .

The chi-squared distribution has one parameter: k — a positive integer that specifies the number of degrees of freedom (i.e. the number of Zi’s)

Read more about this topic:  Chi-squared Distribution

Famous quotes containing the word definition:

    “It is very hard to give a just definition of love. The most we can say of it is this: that in the soul, it is a desire to rule; in the spirit, it is a sympathy; and in the body, it is but a hidden and subtle desire to possess—after many mysteries—what one loves.”
    —François, Duc De La Rochefoucauld (1613–1680)

    “The man who knows governments most completely is he who troubles himself least about a definition which shall give their essence. Enjoying an intimate acquaintance with all their particularities in turn, he would naturally regard an abstract conception in which these were unified as a thing more misleading than enlightening.”
    —William James (1842–1910)

    “No man, not even a doctor, ever gives any other definition of what a nurse should be than this—”devoted and obedient.” This definition would do just as well for a porter. It might even do for a horse. It would not do for a policeman.”
    —Florence Nightingale (1820–1910)