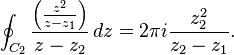Cauchy's Integral Formula - Example

Example

Consider the function

and the contour described by |z| = 2, call it C.

To find the integral of g(z) around the contour, we need to know the singularities of g(z). Observe that we can rewrite g as follows:

where

Clearly the poles become evident, their moduli are less than 2 and thus lie inside the contour and are subject to consideration by the formula. By the Cauchy-Goursat theorem, we can express the integral around the contour as the sum of the integral around z1 and z2 where the contour is a small circle around each pole. Call these contours C1 around z1 and C2 around z2.

Now, around C1, f is analytic (since the contour does not contain the other singularity), and this allows us to write f in the form we require, namely:

and now


\oint_{C_1} \frac{\left(\frac{z^2}{z-z_2}\right)}{z-z_1}\,dz =2\pi i\frac{z_1^2}{z_1-z_2}.

Doing likewise for the other contour:


\oint_{C_2} \frac{\left(\frac{z^2}{z-z_1}\right)}{z-z_2}\,dz =2\pi i\frac{z_2^2}{z_2-z_1}.

The integral around the original contour C then is the sum of these two integrals:

\begin{align} \oint_C \frac{z^2}{z^2+2z+2}\,dz &{}= \oint_{C_1} \frac{\left(\frac{z^2}{z-z_2}\right)}{z-z_1}\,dz + \oint_{C_2} \frac{\left(\frac{z^2}{z-z_1}\right)}{z-z_2}\,dz \\ &{}= 2\pi i\left(\frac{z_1^2}{z_1-z_2}+\frac{z_2^2}{z_2-z_1}\right) \\ &{}= 2\pi i(-2) \\ &{}=-4\pi i. \end{align}


An elementary trick using partial fraction decomposition:

\oint_C g(z)dz =\oint_C \left(1-\frac{1}{z-z_1}-\frac{1}{z-z_2}\right)dz =0-2\pi i-2\pi i =-4\pi i

Read more about this topic:  Cauchy's Integral Formula

Famous quotes containing the word example:

    “Our intellect is not the most subtle, the most powerful, the most appropriate, instrument for revealing the truth. It is life that, little by little, example by example, permits us to see that what is most important to our heart, or to our mind, is learned not by reasoning but through other agencies. Then it is that the intellect, observing their superiority, abdicates its control to them upon reasoned grounds and agrees to become their collaborator and lackey.”
    —Marcel Proust (1871–1922)