Orthographic Projection
When the human eye looks at a scene, objects in the distance appear smaller than objects close by. Orthographic projection ignores this effect to allow the creation of to-scale drawings for construction and engineering.
Orthographic projections are a small set of transforms often used to show profile, detail or precise measurements of a three dimensional object. Common names for orthographic projections include plane, cross-section, bird's-eye, and elevation.
If the normal of the viewing plane (the camera direction) is parallel to one of the primary axes (which is the x, y, or z axis), the mathematical transformation is as follows; To project the 3D point, onto the 2D point, using an orthographic projection parallel to the y axis (profile view), the following equations can be used:
where the vector s is an arbitrary scale factor, and c is an arbitrary offset. These constants are optional, and can be used to properly align the viewport. Using matrix multiplication, the equations become:
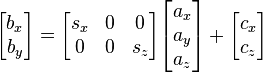 .
.
While orthographically projected images represent the three dimensional nature of the object projected, they do not represent the object as it would be recorded photographically or perceived by a viewer observing it directly. In particular, parallel lengths at all points in an orthographically projected image are of the same scale regardless of whether they are far away or near to the virtual viewer. As a result, lengths near to the viewer are not foreshortened as they would be in a perspective projection.
Read more about this topic: 3D Projection
Famous quotes containing the word projection:
“Those who speak of our culture as dead or dying have a quarrel with life, and I think they cannot understand its terms, but must endlessly repeat the projection of their own desires.”
—Muriel Rukeyser (1913–1980)

